General Information
List of all problems
Last Revised: 4/29/2020 Check back, will be updated over the semester.
For
Sketch these regions in the complex plane:
(a)
(b)Calculate
Calculate the following:
(a)
(b)Solve the following equation for
Which of the following statements is/are true? Explain your answers.
(a)
(b)
(c)If
Show that the equation
With the principal argument given by
(a)
(b)
(c)For which values of
Calculate the following, expressing the result in polar/exponential form,
(a)
(b)
(c)Calculate the following, expressing the result in Cartesian form,
(a)
(b)
(c)Use the “De Moivre identity”
Sketch the following parametric curve:
Find the roots and plot them as points in the complex plane:
(a)
(b)Find all roots and plot them as points in the complex plane for the polynomial
Sketch the set of all points satisfying
Find the real and imaginary parts of the following functions:
(a)
(b)
Hint for (a):Find and sketch the image of a sector of the disk
Find and sketch the image of a ring sector
Find and sketch the image of the unit circle
Show that the function
Use the limit definition of derivative to determine whether the function
Use the Cauchy-Riemann equations written in the form
Are the following functions differentiable anywhere? Are they analytic anywhere? Use Cauchy-Riemann equations
(a)
(b)
(c)Use the usual limit definition of derivative to show that the reciprocal rule holds for complex differentiation, at all points where
Find all values of
(a)
(b)
(c)
(d)Use the usual chain rule to find the derivative of function
Find the Cartesian components (i.e. real and imaginary parts
We learned that any function analytic in some domain yields two solutions of the Laplace’s equation

Find all values of
(a)
(b)Differentiate the function
Use the fundamental theorem of calculus (i.e. find the anti-derivative) to evaluate the following integrals over any contour
(a)
(b)
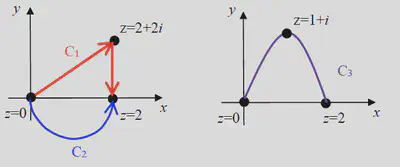
(c)Calculate the following contours integrals (see Figure):
(a)
(b)
(c)
Calculate each integral, or explain why it is equal to zero. Note that all integrals are over circles of given radius. Do not use curve parametrization: use the Cauchy-Goursat Theorem and/or the Fundamental Theorem of Calculus. In (d),
(a)
(b)
(c)
(d)Use Cauchy Integral Formula to calculate the following integrals. You may have to change the contour of integration into a set of closed curves surrounding each singularity inside the contour, as we did in class:
(a)
(b)
(c)Use Cauchy Integral Formula (and/or its higher-order extension) to calculate the following integrals over given circles. You may have to change the contour of integration into a set of closed curves surrounding each singularity inside the contour, as we did in class:
(a)
(b)
(c)
(d)Find the following integral bounds over the given contour:
(a)
(b)Apply the Extended Cauchy Integral Formula
Find the maxima and minima of
Use the ratio test to determine whether this series converges:
Use the ratio test to find the radius of convergence of these power series:
(a)
(b)Prove the Taylor/Maclaurin series
Find the first three non-zero dominant terms in the Taylor series at the given point, and state the radius of convergence of the full series by noting the distance to the nearest singularity:
(a)
(b)
(c)
(d)Find all zeros and poles, and indicate their orders:
(a)
(b)Use series differentiation to find the Taylor series for
Use series integration to find the Taylor series for
Consider the differential equation
Find the Laurent series for
Find the first three dominant terms in the Laurent series for
Find three different series representations for
Classify all singularities of the following functions:
(a)
(b)
(c)Find and classify all singularities inside the integration contour, calculate the residue at each singularity, and then sum the residues to compute the integral:
(a)
(b)
(c)
(d)Evaluate the following integral using inversion mapping (substitution)
Close the contour in the upper half-plane to evaluate the following real integrals:
(a)
(b)Close the contour in the upper half-plane to evaluate the following real integrals. Make sure to indicate which of the two integral calculations requires the use of the Jordan’s Lemma.
(a)
(b)Use the “indented” contour below to finish the integral calculation that we started in class:
Hint: Consider
- First show$$\begin{aligned}&\lim_{R \rightarrow \infty, \rho \rightarrow 0^{+}}\left[\int_{L_{1}} \frac{1-e^{i 2 x}}{2 x^{2}} d x+\int_{L_{2}} \frac{1-e^{i 2 x}}{2 x^{2}} d x\right]\
=&\lim {R \rightarrow \infty , \rho \rightarrow 0^{+}}\left[\int{-R}^{-\rho} \frac{1-e^{i 2 x}}{2 x^{2}} d x+\int_{\rho}^{R} \frac{1-e^{i 2 x}}{2 x^{2}} d x\right].
\end{aligned}
$$ We note that this last integral defines the principal value integral
- Then note that
- Show that
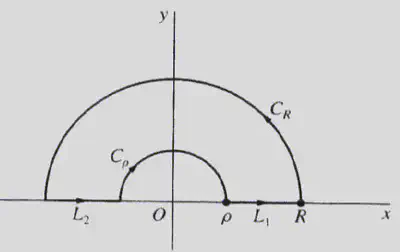
- Here’s another type of contour that is often useful. Use it to integrate
- Where does this have poles?
- Which sides of the rectangle contribute to integral and which sides vanish in the limit
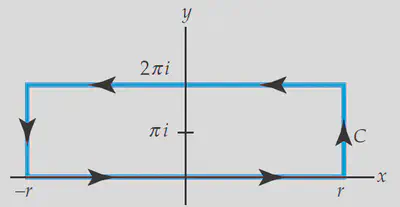
A rectangular contour.
Use the contour from the example in Section 91 to integrate
Use the methods of Section 92 to compute
- (a)
- (b)
